Pyhton 통계

순열과 조합 계산

• 순열: 서로 다른 𝑛개에서 𝑟개를 중복 없이 뽑아 특정한 순서로 나열하는 것을 의미한다.
• 조합: 서로 다른 𝑛개에서 𝑟개를 중복 없이 순서를 고려하지 않고 뽑는 것을 의미한다.
• 중복 순열: 서로 다른 𝑛개에서 중복을 포함해 𝑟개를 뽑아 특정한 순서로 나열하는 것을 의미한다.
• 중복 조합: 서로 다른 𝑛개에서 중복을 포함해 순서를 고려하지 않고 𝑟개를 뽑는 것을 의미한다.

from itertools import permutations

arr = ['A', 'B', 'C']
# 원소 중에서 2개를 뽑는 모든 순열 계산
result = list(permutations(arr, 2))
print(result)

[('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'C'), ('C', 'A'), ('C', 'B')]

from itertools import combinations

arr = ['A', 'B', 'C']
# 원소 중에서 2개를 뽑는 모든 조합 계산
result = list(combinations(arr, 2))
print(result)

[('A', 'B'), ('A', 'C'), ('B', 'C')]

from itertools import product

arr = ['A', 'B', 'C']
# 원소 중에서 2개를 뽑는 모든 중복 순열 계산
result = list(product(arr, repeat=2))
print(result)

[('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'A'), ('B', 'B'), ('B', 'C'), ('C', 'A'), ('C', 'B'), ('C', 'C')]

from itertools import combinations_with_replacement

arr = ['A', 'B', 'C']
# 원소 중에서 2개를 뽑는 모든 중복 조합 계산
result = list(combinations_with_replacement(arr, 2))
print(result)

[('A', 'A'), ('A', 'B'), ('A', 'C'), ('B', 'B'), ('B', 'C'), ('C', 'C')]

이항 분포 시뮬레이션

• 독립된 사건을 𝑁번 반복 시행했을 때, 특정 사건이 𝑥회 발생할 확률을 계산한다.
  • 성공 확률이 𝜇인 베르누이 시행을 𝑁번 반복한다.

from math import factorial
import numpy as np
import matplotlib.pyplot as plt


# PDF (Probability Density Function)
def pdf(x, n, mu):
    combinations = factorial(n) / (factorial(x) * factorial(n - x))
    return combinations * (mu ** x) * ((1 - mu) ** (n - x))


n = 10
mu = 0.1
X = [x for x in range(n + 1)]
prob = [pdf(x, n, mu) for x in X]
plt.bar(X, prob)
plt.show()

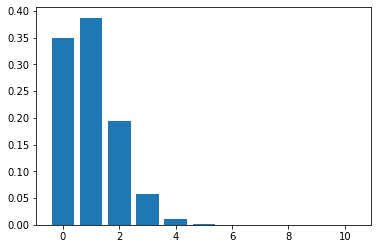
• 가구 공장에서 가구를 만들 때, 불량률이 10%라고 한다.
• 이 공장에서 만든 가구 10개를 확인했을 때, 불량품이 2개 이하로 나올 확률을 구하여라.

n = 10
mu = 0.1
X = [x for x in range(n + 1)]

for x in X:
    print(f"f({x}) = {pdf(x, n, mu) * 100.:.2f}%")

f(0) = 34.87%
f(1) = 38.74%
f(2) = 19.37%
f(3) = 5.74%
f(4) = 1.12%
f(5) = 0.15%
f(6) = 0.01%
f(7) = 0.00%
f(8) = 0.00%
f(9) = 0.00%
f(10) = 0.00%

x0 = pdf(0, 10, 0.1)
x1 = pdf(1, 10, 0.1)
x2 = pdf(2, 10, 0.1)

print(f"가구 10개를 확인했을 때, 불량품이 0개일 확률 = {x0 * 100.:.2f}%")
print(f"가구 10개를 확인했을 때, 불량품이 1개일 확률 = {x1 * 100.:.2f}%")
print(f"가구 10개를 확인했을 때, 불량품이 2개일 확률 = {x2 * 100.:.2f}%")
print(f"가구 10개를 확인했을 때, 불량품이 2개이하일 확률 = {(x0 + x1 + x2) * 100.:.2f}%")

가구 10개를 확인했을 때, 불량품이 0개일 확률 = 34.87%
가구 10개를 확인했을 때, 불량품이 1개일 확률 = 38.74%
가구 10개를 확인했을 때, 불량품이 2개일 확률 = 19.37%
가구 10개를 확인했을 때, 불량품이 2개이하일 확률 = 92.98%

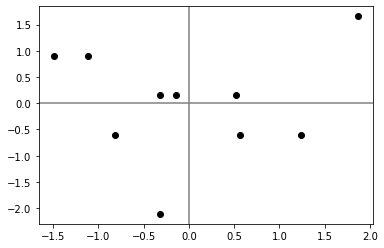
딥러닝 분야의 입력 정규화(Input Normalization)

• 딥러닝 분야에서는 입력 데이터를 정규화하여 학습 속도(training speed)를 개선할 수 있다.

import matplotlib.pyplot as plt

x1 = np.asarray([33, 72, 40, 104, 52, 56, 89, 24, 52, 73])
x2 = np.asarray([9, 8, 7, 10, 5, 8, 7, 9, 8, 7])

normalized_x1 = (x1 - np.mean(x1)) / np.std(x1)
normalized_x2 = (x2 - np.mean(x2)) / np.std(x2)

plt.axvline(x=0, color='gray')
plt.axhline(y=0, color='gray')
plt.scatter(normalized_x1, normalized_x2, color='black')
plt.show()

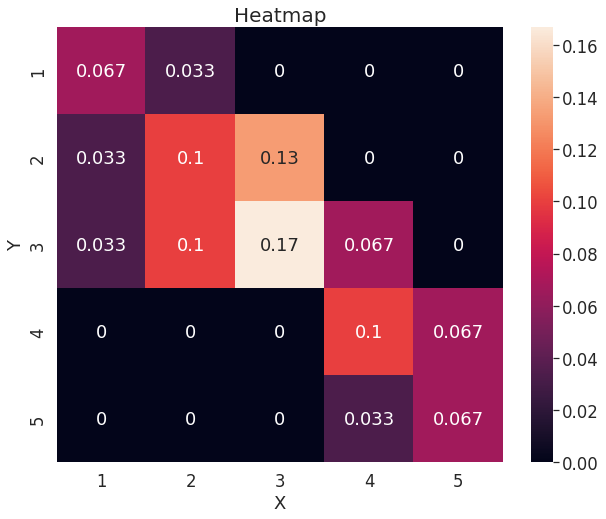
결합 확률 질량 함수(Joint Probability Mass Function) 예시

• 수학 성적($𝑋$)과 영어 성적($𝑌$)에 대한 결합 확률 질량 함수를 나타낼 수 있다.

import pandas as pd


scores = [1, 2, 3, 4, 5]
data = [
    [2, 1, 0, 0, 0],
    [1, 3, 4, 0, 0],
    [1, 3, 5, 2, 0],
    [0, 0, 0, 3, 2],
    [0, 0, 0, 1, 2]
]

# 행(index)과 열(columns) 모두 값으로 [1, 2, 3, 4, 5]를 가진다.
df = pd.DataFrame(data, index=scores, columns=scores)
df.columns.name = "X"
df.index.name = "Y"
pmf = df / df.values.sum()
print(pmf)

X         1         2         3         4         5
Y                                                  
1  0.066667  0.033333  0.000000  0.000000  0.000000
2  0.033333  0.100000  0.133333  0.000000  0.000000
3  0.033333  0.100000  0.166667  0.066667  0.000000
4  0.000000  0.000000  0.000000  0.100000  0.066667
5  0.000000  0.000000  0.000000  0.033333  0.066667

import matplotlib.pyplot as plt
import seaborn as sns


sns.set(font_scale=1.5) # 그림(figure)의 기본적인 폰트(font) 크기 설정
plt.rcParams["figure.figsize"] = [10, 8]
# 히트맵(heatmap) 그리기
ax = sns.heatmap(pmf, annot=True,
    xticklabels=[1, 2, 3, 4, 5],
    yticklabels=[1, 2, 3, 4, 5]
)
plt.title("Heatmap", fontsize=20) # 그림(figure)의 제목(title) 설정
plt.show() 

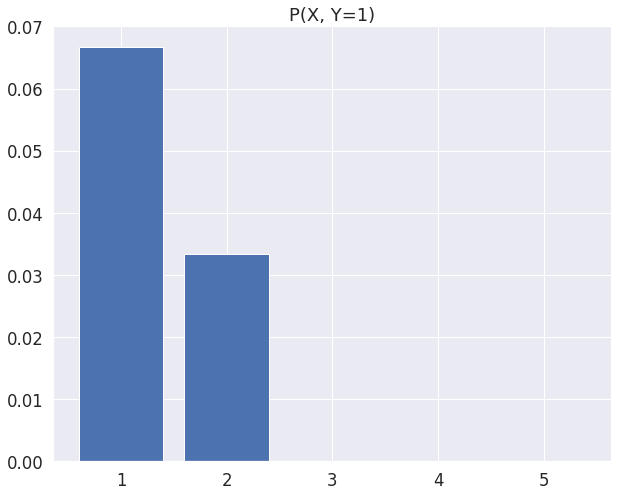
주변 확률 질량 함수(Marginal Probability Mass Function) 예시

• 수학 성적($𝑋$)과 영어 성적($𝑌$)에 대한 주변 확률 질량 함수를 나타낼 수 있다.

index = 0
x = [0, 1, 2, 3, 4]
plt.bar(x, pmf.iloc[index])
plt.xticks(x, ["1", "2", "3", "4", "5"])
plt.title(f"P(X, Y={index + 1})")
plt.show()

# 각 열마다 합계 계산
marginal_pmf_x = pmf.sum(axis=0)
print(marginal_pmf_x)

# 각 행마다 합계 계산
marginal_pmf_y = pmf.sum(axis=1)
print(marginal_pmf_y)

X
1    0.133333
2    0.233333
3    0.300000
4    0.200000
5    0.133333
dtype: float64
Y
1    0.100000
2    0.266667
3    0.366667
4    0.166667
5    0.100000
dtype: float64

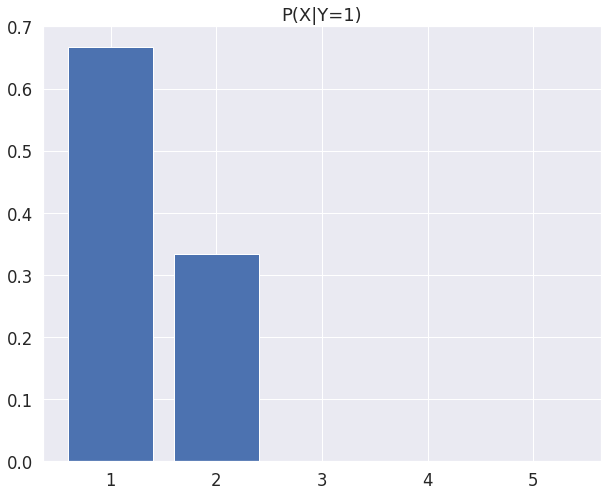
조건부 확률 질량 함수(Conditional Probability Mass Function) 예시

• 수학 성적($𝑋$)과 영어 성적($𝑌$)에 대한 조건부 확률 질량 함수를 나타낼 수 있다.

index = 0
x = [0, 1, 2, 3, 4]
plt.bar(x, pmf.iloc[index] / marginal_pmf_y[index + 1])
plt.xticks(x, ["1", "2", "3", "4", "5"])
plt.title(f"P(X|Y={index + 1})")
plt.show()

평균(Mean), 분산(Variance), 표준 편차(Standard Deviation)

• 학생 성적에 대한 평균, 분산, 표준 편차를 계산하는 예시는 다음과 같다.

import math

arr = [56, 93, 88, 72, 65]

# 평균(mean) 계산
mean = 0
for x in arr:
    mean += x / len(arr)

# 분산(variance) 계산
variance = 0
for x in arr:
    variance += ((x - mean) ** 2) / len(arr)

# 표준 편차(standard deviation) 계산
std = math.sqrt(variance)

print(f"평균: {mean:.2f}")
print(f"분산: {variance:.2f}")
print(f"표준 편차: {std:.2f}")

평균: 74.80
분산: 192.56
표준 편차: 13.88

import math

arr = [41, 100, 90, 63, 80]

# 평균(mean) 계산
mean = 0
for x in arr:
    mean += x / len(arr)

# 분산(variance) 계산
variance = 0
for x in arr:
    variance += ((x - mean) ** 2) / len(arr)

# 표준 편차(standard deviation) 계산
std = math.sqrt(variance)

print(f"평균: {mean:.2f}")
print(f"분산: {variance:.2f}")
print(f"표준 편차: {std:.2f}")

평균: 74.80
분산: 434.96
표준 편차: 20.86

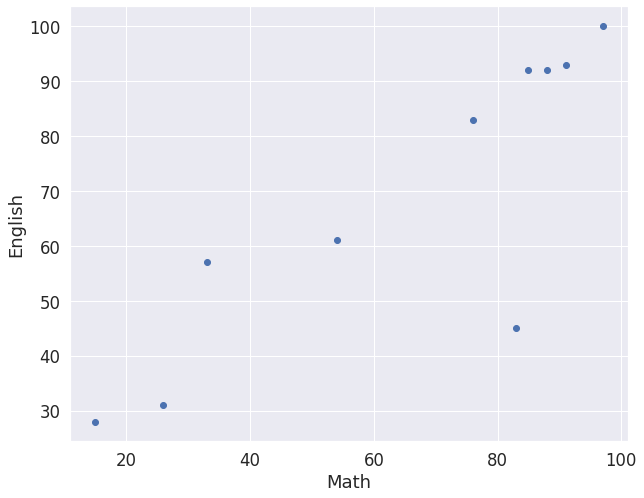
공분산(Covariance)과 상관계수(Correlation Coefficient)

• 공분산도 분산과 마찬가지로 데이터가 평균으로부터 얼마나 멀리 떨어져있는지 나타내기 위해 사용한다.
• 수학 성적과 영어 성적에 대하여 평균, 분산, 공분산, 상관계수를 계산할 수 있다.

import matplotlib.pyplot as plt

X = [97, 85, 26, 54, 76, 15, 33, 83, 88, 91]
Y = [100, 92, 31, 61, 83, 28, 57, 45, 92, 93]
plt.plot(X, Y, 'o')
plt.xlabel("Math")
plt.ylabel("English")
plt.show()

# 평균(mean) 계산
x_mean = 0
for x in X:
    x_mean += x / len(X)
# 분산(variance) 계산
x_var = 0
for x in X:
    x_var += ((x - x_mean) ** 2) / (len(X) - 1)

print(f"x_mean = {x_mean:.3f}, x_var = {x_var:.3f}")

# 평균(mean) 계산
y_mean = 0
for y in Y:
    y_mean += y / len(Y)
# 분산(variance) 계산
y_var = 0
for y in Y:
    y_var += ((y - y_mean) ** 2) / (len(Y) - 1)
    
print(f"y_mean = {y_mean:.3f}, y_var = {y_var:.3f}")

x_mean = 64.800, x_var = 915.511
y_mean = 68.200, y_var = 743.733

import numpy as np
np.set_printoptions(precision=3)
import math

# 공분산(covariance)
covar = 0
for x, y in zip(X, Y):
    covar += ((x - x_mean) * (y - y_mean)) / (len(X) - 1)
print(f"Sample covariance: {covar:.3f}")
print("[Sample covariance (NumPy)]")
print(np.cov(X, Y))

# 상관 계수(correlation coefficient)
correlation_coefficient = covar / math.sqrt(x_var * y_var)
print(f"Correlation coefficient: {correlation_coefficient:.3f}")
print("[Correlation coefficient (NumPy)]")
print(np.corrcoef(X, Y))

Sample covariance: 703.267
[Sample covariance (NumPy)]
[[915.511 703.267]
 [703.267 743.733]]
Correlation coefficient: 0.852
[Correlation coefficient (NumPy)]
[[1.    0.852]
 [0.852 1.   ]]

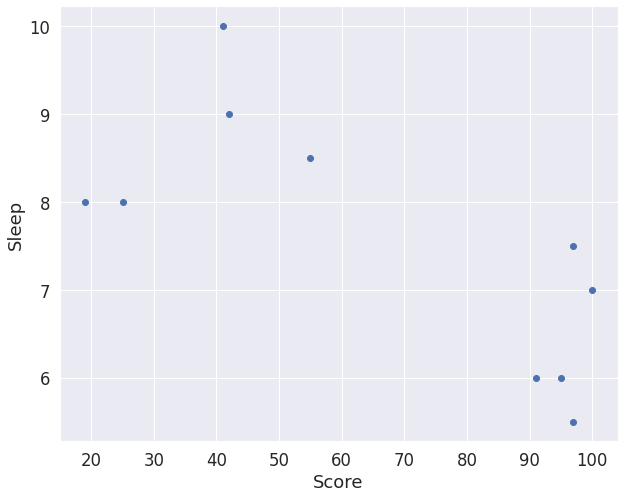
• 성적과 수면 시간에 대하여 평균, 분산, 공분산, 상관계수를 계산할 수 있다.

import matplotlib.pyplot as plt

X = [97, 100, 25, 42, 55, 19, 41, 97, 95, 91]
Y = [5.5, 7, 8, 9, 8.5, 8, 10, 7.5, 6, 6]
plt.plot(X, Y, 'o')
plt.xlabel("Score")
plt.ylabel("Sleep")
plt.show()

# 평균(mean) 계산
x_mean = 0
for x in X:
    x_mean += x / len(X)
# 분산(variance) 계산
x_var = 0
for x in X:
    x_var += ((x - x_mean) ** 2) / (len(X) - 1)

print(f"x_mean = {x_mean:.3f}, x_var = {x_var:.3f}")

# 평균(mean) 계산
y_mean = 0
for y in Y:
    y_mean += y / len(Y)
# 분산(variance) 계산
y_var = 0
for y in Y:
    y_var += ((y - y_mean) ** 2) / (len(Y) - 1)
    
print(f"y_mean = {y_mean:.3f}, y_var = {y_var:.3f}")

x_mean = 66.200, x_var = 1083.956
y_mean = 7.550, y_var = 2.081

import numpy as np
np.set_printoptions(precision=3)
import math

# 공분산(covariance)
covar = 0
for x, y in zip(X, Y):
    covar += ((x - x_mean) * (y - y_mean)) / (len(X) - 1)
print(f"Sample covariance: {covar:.3f}")
print("[Sample covariance (NumPy)]")
print(np.cov(X, Y))

# 상관 계수(correlation coefficient)
correlation_coefficient = covar / math.sqrt(x_var * y_var)
print(f"Correlation coefficient: {correlation_coefficient:.3f}")
print("[Correlation coefficient (NumPy)]")
print(np.corrcoef(X, Y))

Sample covariance: -34.844
[Sample covariance (NumPy)]
[[1083.956  -34.844]
 [ -34.844    2.081]]
Correlation coefficient: -0.734
[Correlation coefficient (NumPy)]
[[ 1.    -0.734]
 [-0.734  1.   ]]

모멘트 방법을 활용한 정규 분포의 추정

• 평균(1차 모멘트)과 분산(2차 모멘트)를 활용해 정규 분포를 추정할 수 있다.

import math

arr = [1] * 3 + [2] * 5 + [3] * 7 + [4] * 10 + [5] * 6 + [6] * 6 + [7] * 3

# 평균(mean) 계산
mean = 0
for x in arr:
    mean += x / len(arr)

# 분산(variance) 계산
variance = 0
for x in arr:
    variance += ((x - mean) ** 2) / len(arr)

# 표준 편차(standard deviation) 계산
std = math.sqrt(variance)

print(f"평균: {mean:.3f}")
print(f"분산: {variance:.3f}")
print(f"표준 편차: {std:.3f}")

평균: 4.025
분산: 2.774
표준 편차: 1.666

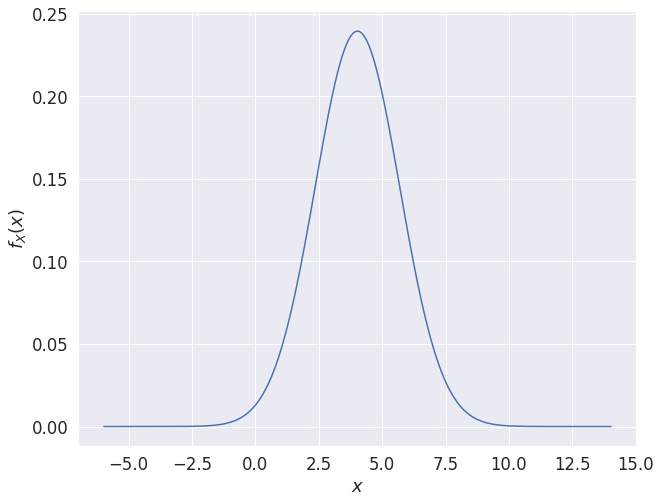
import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = [10, 8]

# 평균(mean)을 중심으로 다수의 x 데이터 생성
x = np.linspace(mean - 10, mean + 10, 1000)
# 정규 분포의 확률 밀도 함수(probability density function)
y = (1 / (np.sqrt(2 * np.pi) * std)) * np.exp(-1 / (2 * (std ** 2)) * ((x - mean) ** 2))
plt.plot(x, y)
plt.xlabel("$x$")
plt.ylabel("$f_X(x)$")
plt.show()

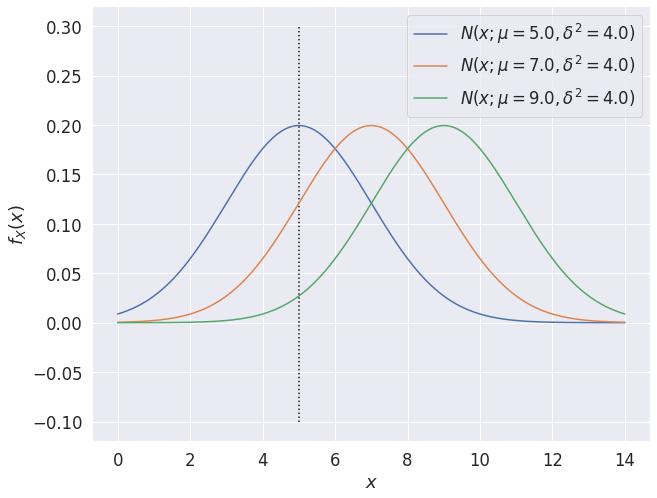
최대 가능도 추정

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["figure.figsize"] = [10, 8]
plt.rcParams["font.size"] = "16"

# 정규 분포 확률 밀도 함수(probability density function)
def pdf(x, mean, std):
    result = 1 / (np.sqrt(2 * np.pi) * std)
    result *= np.exp(-1 / (2 * (std ** 2)) * ((x - mean) ** 2))
    return result

x = np.linspace(0, 14, 1000)
std = 2 # 알고 있는 정보(variance)
data = 5 # 가지고 있는 데이터
for mean in [5, 7, 9]:
    y = pdf(x, mean, std)
    plt.plot(x, y, label=f"$N(x;\mu={mean:.1f},\delta^2={std ** 2:.1f})$")

plt.vlines(data, -0.1, 0.3, linestyle=":")
plt.xlabel("$x$")
plt.ylabel("$f_X(x)$")
plt.legend()
plt.show()

데이터 추출(Data Sampling)

• 리스트 내에서 1개의 원소만 랜덤으로 추출할 수 있다.

import random

arr = [1, 2, 3, 4, 5]
sampled = random.choice(arr)
print(sampled)

3

• 리스트 내에서 k개의 원소를 중복 없이 랜덤으로 추출할 수 있다.

import random

arr = [1, 2, 3, 4, 5]
sampled = random.sample(arr, 3)
print(sampled)

[4, 2, 1]

• 리스트 내에서 k개의 원소를 중복을 허용하여 랜덤으로 추출할 수 있다.

import random

arr = [1, 2, 3, 4, 5]
sampled = [random.choice(arr) for i in range(3)]
print(sampled)

[4, 4, 5]

import random

arr = [1, 2, 3, 4, 5]
sampled = random.choices(arr, k=3)
print(sampled)

[3, 1, 5]

import random

arr = [1, 2, 3, 4, 5]
# 중복을 허용하기 때문에, k가 원소의 개수보다 클 수 있다.
sampled = random.choices(arr, k=7)
print(sampled)

[1, 3, 3, 5, 1, 1, 4]

• [0,1] 범위의 균등 분포에서 5개의 데이터를 추출할 수 있다.

import numpy as np

sampled = np.random.uniform(0, 1, 5)
print(sampled)

[0.071 0.375 0.029 0.341 0.637]

• 표준 정규 분포(평균: 0, 표준편차: 1)에서 5개의 데이터를 추출한다.

import numpy as np

sampled = np.random.normal(0, 1, 5)
print(sampled)

[ 0.167 -0.129 -0.432 -0.592  1.545]