Boston House Prices
프로젝트 명: 앙상블 기법을 활용한 보스톤 주택 가격 예측 (Boston House Prices)
보스톤 주택 가격과 관련된 데이터를 기반으로 주택 가격을 예측합니다.
데이터 출처: Boston House Prices
원본출처: UCI ML housing dataset
본 데이터셋은 scikit-learn 패키지의 load_boston을 활용하여 로드하는 데이터셋이며 원본 출처는 카네기 멜론 대학에서 운영하고 있는 the StatLib library에서 발췌하였습니다.
프로젝트 개요
데이터베이스의 각 레코드는 보스턴 교외 또는 도시를 설명합니다. 여러분들은 주어진 13개의 데이터 컬럼을 바탕으로 주택 가격을 예측해야 합니다. 이 데이터는 1970 년 보스턴 표준 메트로폴리탄 통계 지역 (SMSA)에서 발췌 한 것입니다.
프로젝트 목표
1. 데이터 시각화를 통한 데이터 특성을 파악합니다.
2. `pandas`, `numpy`, `scikit-learn` 패키지를 활용하여 데이터 가공, 전처리, 피처 공학(feature engineering)을 진행합니다.
3. 회귀문제를 다루는 **머신러닝 앙상블 기법**을 활용하여 **보스톤 주택 가격 예측**을 진행합니다.
4. 다양한 머신러닝 모델을 구현해보고, 보스톤 주택 가격 데이터셋으로 가격예측 모델을 만들어 성능을 비교 합니다.
5. 각기 다른 모델을 활용하여 앙상블 모델을 구현 및 성능을 비교합니다.
프로젝트 구성
* 데이터 로드 (load data)
* 데이터 시각화 (visualization)
* 데이터 전처리 (pre-processing)
* 머신러닝 모델링 (개별 모델링)
* 평가지표 생성 (evalutation)
* Bagging, Boosting, Voting, Stacking 기법을 활용하여 앙상블 모델 완성
- 작성자: 이경록 감수자
데이터
컬럼 소개
속성 수 : 13
- CRIM: 범죄율
- ZN: 25,000 평방 피트 당 주거용 토지의 비율
- INDUS: 비소매(non-retail) 비즈니스 면적 비율
- CHAS: 찰스 강 더미 변수 (통로가 하천을 향하면 1; 그렇지 않으면 0)
- NOX: 산화 질소 농도 (천만 분의 1)
- RM:주거 당 평균 객실 수
- AGE: 1940 년 이전에 건축된 자가 소유 점유 비율
- DIS: 5 개의 보스턴 고용 센터까지의 가중 거리
- RAD: 고속도로 접근성 지수
- TAX: 10,000 달러 당 전체 가치 재산 세율
- PTRATIO 도시 별 학생-교사 비율
- B: 1000 (Bk-0.63) ^ 2 여기서 Bk는 도시 별 검정 비율입니다.
- LSTAT: 인구의 낮은 지위
- MEDV: 자가 주택의 중앙값 (1,000 달러 단위)
목표
- 학습을 위한 train / 검증을 위한 test 셋으로 분리합니다.
- 검증을 위한 평가지표를 만듭니다.
- 단일 classifiction 모델로 baseline 예측 성능 획득: 가장 기본적인 classification 모델로 baseline 예측율을 얻습니다.
- boosting 계열의 앙상블 모델을 활용하여 예측 성능을 측정합니다.
- voting 계열의 앙상블 모델을 활용하여 예측 성능을 측정합니다.
- bagging 계열의 앙상블 모델을 활용하여 예측 성능을 측정합니다.
- 앙상블 모델과 앙상블 모델을 섞는 blending ensemble 기법을 적용합니다.
- 모델을 쌓아올리는 stacking ensemble 기법을 적용합니다.
출처
-
Harrison, D. and Rubinfeld, D.L. (1978) Hedonic prices and the demand for clean air. J. Environ. Economics and Management 5, 81–102.
-
Belsley D.A., Kuh, E. and Welsch, R.E. (1980) Regression Diagnostics. Identifying Influential Data and Sources of Collinearity. New York: Wiley.
데이터 셋 로드
from sklearn.datasets import load_boston
# 데이터셋 로드
boston = load_boston()
# 데이터셋의 description 출력
print(boston.DESCR)
.. _boston_dataset:
Boston house prices dataset
---------------------------
**Data Set Characteristics:**
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
.. topic:: References
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
import pandas as pd
import numpy as np
import warnings
warnings.filterwarnings('ignore')
# 랜덤 시드 고정
SEED = 34
- X: Feature 데이터 입니다.
- Y: 집 값이며, 우리가 예측할 Target 데이터 입니다.
X = pd.DataFrame(boston['data'], columns=boston['feature_names'])
Y = pd.Series(boston['target'])
X.head()
| CRIM | ZN | INDUS | CHAS | NOX | RM | AGE | DIS | RAD | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.0 | 0.538 | 6.575 | 65.2 | 4.0900 | 1.0 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.0 | 0.469 | 6.421 | 78.9 | 4.9671 | 2.0 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.0 | 0.469 | 7.185 | 61.1 | 4.9671 | 2.0 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.0 | 0.458 | 6.998 | 45.8 | 6.0622 | 3.0 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.0 | 0.458 | 7.147 | 54.2 | 6.0622 | 3.0 | 222.0 | 18.7 | 396.90 | 5.33 |
Y.head()
0 24.0
1 21.6
2 34.7
3 33.4
4 36.2
dtype: float64
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import seaborn as sns
# 한글폰트 로딩
plt.rcParams['font.family'] = 'NanumGothic'
%matplotlib inline
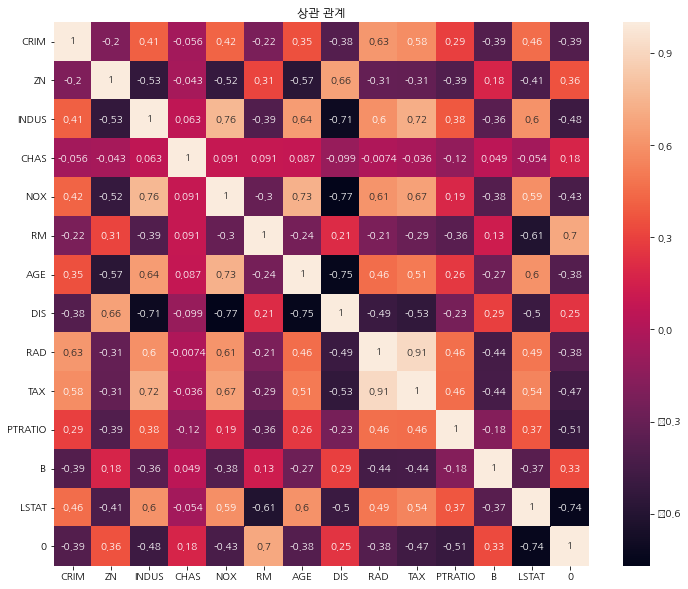
각 컬럼간의 상관관계를 확인합니다.
- 0에 가까울 수록 상관관계가 없습니다.
- 1에 가까울 수록 비례관계를 갖습니다.
- -1에 가까울 수록 반비례관계를 갖습니다.
df = pd.concat([X, Y], axis=1)
plt.figure(figsize=(12, 10))
sns.heatmap(df.corr(), annot=True)
plt.title('상관 관계')
plt.show()
데이터 셋 분할 (train / test)
자세한 사항은 train_test_split 모듈을 활용하여 학습과 테스트 세트 분리 를 참고해 보시기 바랍니다.
from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(df, Y, test_size=0.3, random_state=SEED)
print(x_train.shape, x_test.shape)
(354, 14) (152, 14)
평가 지표 만들기
아래 코드는 수정하지 않아도 됩니다.
평가 지표를 활용하여 앞으로 진행될 실습에 대한 평가를 진행합니다.
prediction에 모델이 예측한 주택 가격을 넣으면, Mean Squared Error를 보여줍니다.
prediction에 name 인자에 알고리즘 이름을 넣어주면, 알아서 저장하여 모두 시각화하여 출력해 줍니다.
from sklearn.metrics import mean_squared_error
my_prediction = {}
colors = ['r', 'c', 'm', 'y', 'k', 'khaki', 'teal', 'orchid', 'sandybrown',
'greenyellow', 'dodgerblue', 'deepskyblue', 'rosybrown', 'firebrick',
'deeppink', 'crimson', 'salmon', 'darkred', 'olivedrab', 'olive',
'forestgreen', 'royalblue', 'indigo', 'navy', 'mediumpurple', 'chocolate',
'gold', 'darkorange', 'seagreen', 'turquoise', 'steelblue', 'slategray',
'peru', 'midnightblue', 'slateblue', 'dimgray', 'cadetblue', 'tomato'
]
def evaluate_prediction(prediction, name='no_name'):
global my_prediction
global y_test
global colors
mse = mean_squared_error(prediction, y_test)
my_prediction[name] = mse
y_value = sorted(my_prediction.items(), key=lambda x: x[1], reverse=True)
df = pd.DataFrame(y_value, columns=['algorithm', 'mse'])
print(df)
min_ = df['mse'].min() - 10
max_ = df['mse'].max() + 10
length = len(df)
plt.figure(figsize=(10, length))
ax = plt.subplot()
ax.set_yticks(np.arange(len(df)))
ax.set_yticklabels(df['algorithm'], fontsize=15)
bars = ax.barh(np.arange(len(df)), df['mse'])
for i, v in enumerate(df['mse']):
idx = np.random.choice(len(colors))
bars[i].set_color(colors[idx])
ax.text(v + 2, i, str(round(v, 3)), color='k', fontsize=15, fontweight='bold')
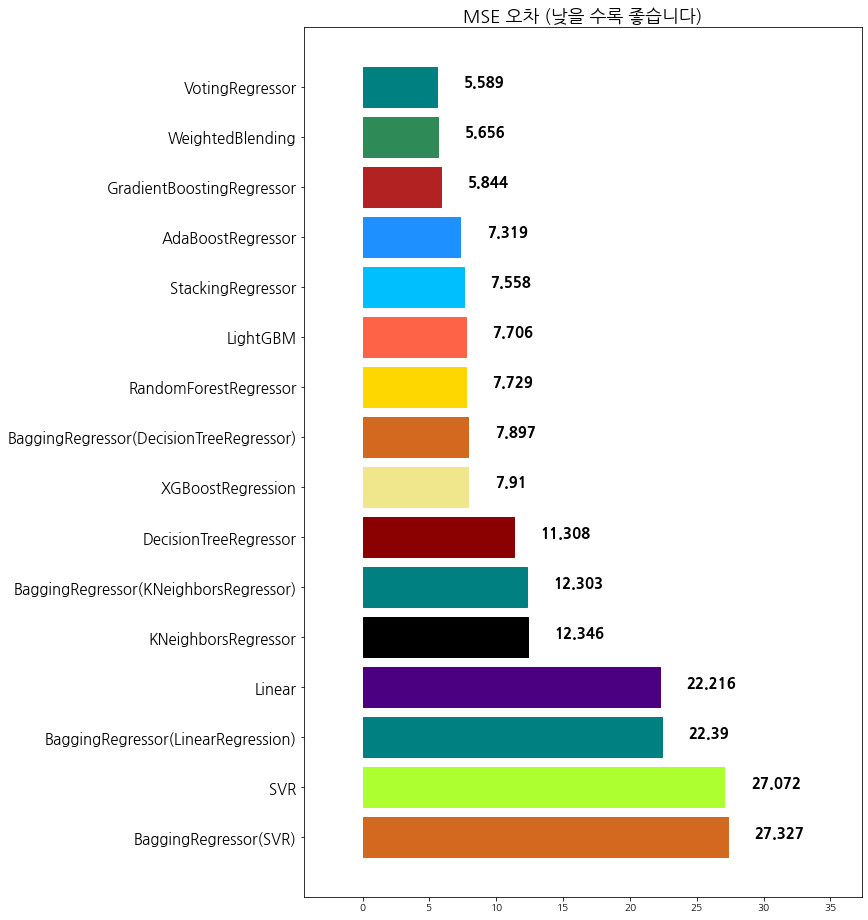
plt.title('MSE 오차 (낮을 수록 좋습니다)', fontsize=18)
plt.xlim(min_, max_)
plt.show()
Q1. 단일 회귀 모델을 활용하여 주택 가격 예측
scikit-learn 라이브러리를 활용하여 주택 가격 예측을 진행해보고, evaluate_prediction을 통해 시각화를 진행합니다.
** 과제 1 **
KNeighborsRegressor를 활용하여 주택 가격을 예측합니다.- hyperparameter는 아무것도 지정하지 않습니다.
knr_pred변수에 예측 값을 대입해주세요- 점수는 26 보다 아래가 나와야 PASS 입니다.
# 코드를 입력하세요
from sklearn.neighbors import KNeighborsRegressor
clf1 = KNeighborsRegressor()
clf1.fit(x_train, y_train)
# 예측 값을 대입해 주세요
knr_pred = clf1.predict(x_test)
아래 코드는 수정하지 말고 실행만 해주세요
evaluate_prediction(knr_pred, 'KNeighborsRegressor')
algorithm mse
0 KNeighborsRegressor 24.542374

아직 예측율이 그 다지 좋지 못합니다.
모델을 바꾸는 방법도 있지만, 그전에 전처리를 잘 해주는 것이 중요합니다.
아무런, 전처리를 해주지 않은 상황과 간단한 전처리만으로 얼마나 모델성능이 개선되는지 확인해 봅시다.
간단한 column 전처리
다음 3가지의 전처리를 진행하겠습니다.
- 카테고리형 column과 수치형 column 분리
- 카테고리형 column에 대하여 category 타입 변환
- 변환된 column을 원핫 인코딩
- 수치형 데이터에 대하여 StandardScaling
먼저, 각 컬럼별 데이터의 value 종류를 파악해 보겠습니다.
value_counts() 메소드를 활용하면 매우 쉽게 알아볼 수 있습니다.
col_dict = {}
for col in X.columns:
print('column: {}, value_counts: {}'.format(col, len(X[col].value_counts())))
col_dict[col] = len(X[col].value_counts())
column: CRIM, value_counts: 504
column: ZN, value_counts: 26
column: INDUS, value_counts: 76
column: CHAS, value_counts: 2
column: NOX, value_counts: 81
column: RM, value_counts: 446
column: AGE, value_counts: 356
column: DIS, value_counts: 412
column: RAD, value_counts: 9
column: TAX, value_counts: 66
column: PTRATIO, value_counts: 46
column: B, value_counts: 357
column: LSTAT, value_counts: 455
plt.figure(figsize=(10, 6))
plt.bar(col_dict.keys(), col_dict.values())
plt.title('column 별 value_counts()')
plt.show()
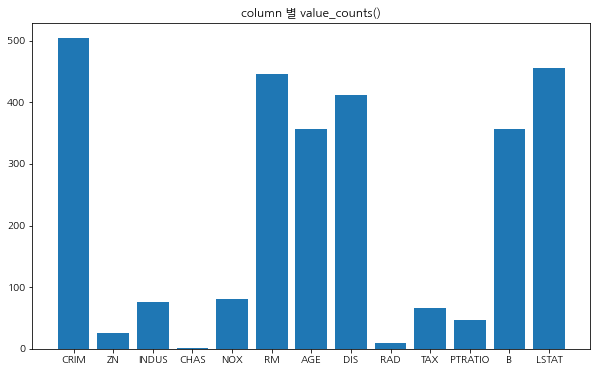
각 column에 대하여 얼마나 다양한 종류의 데이터로 구성되어 있는지 확인해 봤습니다.
아무래도 CHAS 컬럼은 2개의 데이터 종류가 RAD 컬럼은 9개의 데이터 종류가 있습니다.
컬럼의 내용을 보면 다음과 같습니다.
- CHAS: 찰스 강 더미 변수 (통로가 하천을 향하면 1; 그렇지 않으면 0)
- RAD: 고속도로 접근성 지수
CHAS는 Boolean 형태이므로 우리는 수치형이 아닌 카테고리 형 컬럼이라고 단정지어도 되겠습니다.
RAD는 고속도로 접근성 지수인데, 굳이 수치형이 아니더라도 가령 매우 좋음 ~ 매우 나쁨 처럼 평점정도로 생각하고 카테고리형 데이터 컬럼으로 취급해 보도록 하겠습니다. 게다가 종류가 9개 밖에 되지 않으니깐요.
cat_cols = ['CHAS', 'RAD']
# 카테고리형 데이터프레임
df_category = pd.DataFrame()
for col in cat_cols:
df_category[col] = X[col].astype('category')
# 수치형 데이터프레임
num_cols = [col for col in X.columns if col not in cat_cols]
df_numerical = X[num_cols]
df_category.head()
| CHAS | RAD | |
|---|---|---|
| 0 | 0.0 | 1.0 |
| 1 | 0.0 | 2.0 |
| 2 | 0.0 | 2.0 |
| 3 | 0.0 | 3.0 |
| 4 | 0.0 | 3.0 |
df_numerical.head()
| CRIM | ZN | INDUS | NOX | RM | AGE | DIS | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.00632 | 18.0 | 2.31 | 0.538 | 6.575 | 65.2 | 4.0900 | 296.0 | 15.3 | 396.90 | 4.98 |
| 1 | 0.02731 | 0.0 | 7.07 | 0.469 | 6.421 | 78.9 | 4.9671 | 242.0 | 17.8 | 396.90 | 9.14 |
| 2 | 0.02729 | 0.0 | 7.07 | 0.469 | 7.185 | 61.1 | 4.9671 | 242.0 | 17.8 | 392.83 | 4.03 |
| 3 | 0.03237 | 0.0 | 2.18 | 0.458 | 6.998 | 45.8 | 6.0622 | 222.0 | 18.7 | 394.63 | 2.94 |
| 4 | 0.06905 | 0.0 | 2.18 | 0.458 | 7.147 | 54.2 | 6.0622 | 222.0 | 18.7 | 396.90 | 5.33 |
자, 이제 카테고리형 컬럼과 수치형 컬럼으로 분류해보았습니다.
카테고리형 데이터프레임에는 원핫인코딩을 진행하고,
수치형 데이터프레임에는 StandardScaling을 진행하겠습니다.
df_category = pd.get_dummies(df_category)
df_category
| CHAS_0.0 | CHAS_1.0 | RAD_1.0 | RAD_2.0 | RAD_3.0 | RAD_4.0 | RAD_5.0 | RAD_6.0 | RAD_7.0 | RAD_8.0 | RAD_24.0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 502 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 503 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 504 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 505 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
506 rows × 11 columns
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaled = scaler.fit_transform(df_numerical)
df_numerical = pd.DataFrame(scaled, columns=df_numerical.columns)
df_numerical
| CRIM | ZN | INDUS | NOX | RM | AGE | DIS | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -0.419782 | 0.284830 | -1.287909 | -0.144217 | 0.413672 | -0.120013 | 0.140214 | -0.666608 | -1.459000 | 0.441052 | -1.075562 |
| 1 | -0.417339 | -0.487722 | -0.593381 | -0.740262 | 0.194274 | 0.367166 | 0.557160 | -0.987329 | -0.303094 | 0.441052 | -0.492439 |
| 2 | -0.417342 | -0.487722 | -0.593381 | -0.740262 | 1.282714 | -0.265812 | 0.557160 | -0.987329 | -0.303094 | 0.396427 | -1.208727 |
| 3 | -0.416750 | -0.487722 | -1.306878 | -0.835284 | 1.016303 | -0.809889 | 1.077737 | -1.106115 | 0.113032 | 0.416163 | -1.361517 |
| 4 | -0.412482 | -0.487722 | -1.306878 | -0.835284 | 1.228577 | -0.511180 | 1.077737 | -1.106115 | 0.113032 | 0.441052 | -1.026501 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 501 | -0.413229 | -0.487722 | 0.115738 | 0.158124 | 0.439316 | 0.018673 | -0.625796 | -0.803212 | 1.176466 | 0.387217 | -0.418147 |
| 502 | -0.415249 | -0.487722 | 0.115738 | 0.158124 | -0.234548 | 0.288933 | -0.716639 | -0.803212 | 1.176466 | 0.441052 | -0.500850 |
| 503 | -0.413447 | -0.487722 | 0.115738 | 0.158124 | 0.984960 | 0.797449 | -0.773684 | -0.803212 | 1.176466 | 0.441052 | -0.983048 |
| 504 | -0.407764 | -0.487722 | 0.115738 | 0.158124 | 0.725672 | 0.736996 | -0.668437 | -0.803212 | 1.176466 | 0.403225 | -0.865302 |
| 505 | -0.415000 | -0.487722 | 0.115738 | 0.158124 | -0.362767 | 0.434732 | -0.613246 | -0.803212 | 1.176466 | 0.441052 | -0.669058 |
506 rows × 11 columns
전처리가 끝났으니, 두개의 데이터프레임을 다시 합쳐주겠습니다.
df = pd.concat([df_category, df_numerical], axis=1)
df.head()
| CHAS_0.0 | CHAS_1.0 | RAD_1.0 | RAD_2.0 | RAD_3.0 | RAD_4.0 | RAD_5.0 | RAD_6.0 | RAD_7.0 | RAD_8.0 | ... | ZN | INDUS | NOX | RM | AGE | DIS | TAX | PTRATIO | B | LSTAT | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 0.284830 | -1.287909 | -0.144217 | 0.413672 | -0.120013 | 0.140214 | -0.666608 | -1.459000 | 0.441052 | -1.075562 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ... | -0.487722 | -0.593381 | -0.740262 | 0.194274 | 0.367166 | 0.557160 | -0.987329 | -0.303094 | 0.441052 | -0.492439 |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | ... | -0.487722 | -0.593381 | -0.740262 | 1.282714 | -0.265812 | 0.557160 | -0.987329 | -0.303094 | 0.396427 | -1.208727 |
| 3 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... | -0.487722 | -1.306878 | -0.835284 | 1.016303 | -0.809889 | 1.077737 | -1.106115 | 0.113032 | 0.416163 | -1.361517 |
| 4 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | ... | -0.487722 | -1.306878 | -0.835284 | 1.228577 | -0.511180 | 1.077737 | -1.106115 | 0.113032 | 0.441052 | -1.026501 |
5 rows × 22 columns
print(df.shape)
# output
# (506, 22)
(506, 22)
x_train, x_test, y_train, y_test = train_test_split(df, Y, test_size=0.3, random_state=SEED)
전처리를 진행한 데이터셋으로 다시 예측을 진행합니다.
마찬가지로 KNeighborsRegressor로 예측하며, evaluate_prediction을 통해 시각화를 진행합니다.
이전 결과와 어떻게 달라졌는지 비교합니다.
Q2. KNeighborsRegressor를 활용하여 예측
KNeighborsRegressor를 활용하여 주택 가격을 예측합니다.- hyperparameter는 아무것도 지정하지 않습니다.
knr_pred_2변수에 예측 값을 대입해주세요- 점수는 15 보다 아래가 나와야 PASS 입니다.
# 코드를 입력하세요
knr = KNeighborsRegressor()
knr.fit(x_train, y_train)
# 예측 값을 대입해 주세요
knr_pred_2 = knr.predict(x_test)
evaluate_prediction(knr_pred_2, 'KNeighborsRegressor')
algorithm mse
0 KNeighborsRegressor 12.345947

어때요. 모델 성능의 개선이 눈에 보이시나요?
from sklearn.linear_model import LinearRegression
lin = LinearRegression()
lin.fit(x_train, y_train)
lin_pred = lin.predict(x_test)
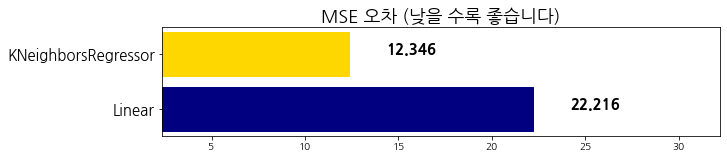
evaluate_prediction(lin_pred, 'Linear')
algorithm mse
0 Linear 22.215878
1 KNeighborsRegressor 12.345947
from sklearn.svm import SVR
svr = SVR()
svr.fit(x_train, y_train)
svr_pred = svr.predict(x_test)
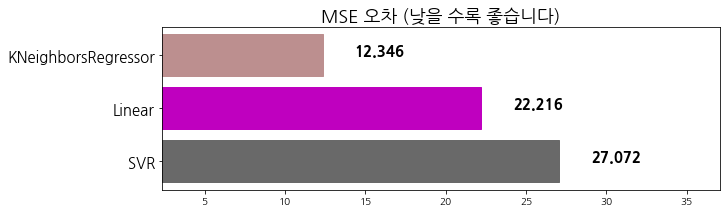
evaluate_prediction(svr_pred, 'SVR')
algorithm mse
0 SVR 27.072338
1 Linear 22.215878
2 KNeighborsRegressor 12.345947
from sklearn.tree import DecisionTreeRegressor
dtr = DecisionTreeRegressor()
dtr.fit(x_train, y_train)
dtr_pred = dtr.predict(x_test)
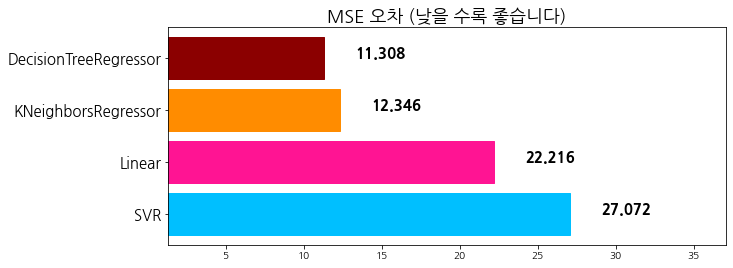
evaluate_prediction(dtr_pred, 'DecisionTreeRegressor')
algorithm mse
0 SVR 27.072338
1 Linear 22.215878
2 KNeighborsRegressor 12.345947
3 DecisionTreeRegressor 11.307961
Bagging 앙상블
from IPython.display import Image
Image('https://teddylee777.github.io/images/2019-12-17/image-20191217015537872.png')
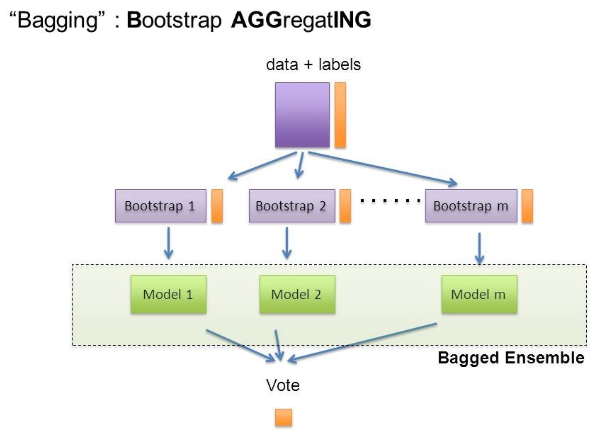
Bagging 이란 Bagging은 Bootstrap Aggregating의 줄임말입니다.
- Bootstrap = Sample(샘플)
- Aggregating = 합산
이라고 풀이할 수 있겠습니다.
Bootstrap은 여러 개의 dataset을 중첩을 허용하게 하여 샘플링하여 분할하는 방식을 말합니다.
Bagging 앙상블의 장점
Bagging 기법을 활용하며 단일 model을 활용하여 prediction (예측)을 했을 때보다 variance(분산) 를 줄이는 효과를 볼 수 있습니다.
model의 학습 오류는 대부분 3가지 주요 원인으로 볼 수 있는데, 바로 분산, 노이즈, 그리고 편향(bias) 입니다. (물론 overfitting/underfitting 그리고 다양한 전처리 이슈들이 더욱 중요하게 다뤄지지만 그 부분들은 setting이 되었다고 가정하겠습니다)
Bagging 앙상블을 통해 분산을 줄여 최종 결과물의 성능을 올릴 수 있습니다.
더 많은 내용은 앙상블 학습(ensemble learning)으로 알고리즘 성능 개선하기 - Bagging 에서 확인할 수 있습니다.
Q3. BaggingRegressor를 활용해서 주택가격 예측하기
- Base Estimator를 LinearRegression, SVR, DecisionTree, KNeighborsRegressor를 사용
n_estimators=100 으로 고정random_state=SEED 로 고정
n_estimators는 의사 결정 나무의 숫자를 의미합니다.
앙상블을 할 때 50명의 의견을 듣고 결정하는 상황과, 100명의 의견을 듣고 결정하는 상황에서 최종 판단의 결과가 다르게 나오듯, 앙상블에서도 의사 결정에 영향을 주는 n_estimators 파라미터의 설정이 매우 중요합니다.
단, 무조건 숫자가 크다고 좋은 것은 아닙니다. 오버피팅을 초래할 수 있습니다.
from sklearn.ensemble import BaggingRegressor
Q3-1. base_estimator는 LinearRegression
예측 결과 값은 br_pred_linear 변수에 대입해 주세요
## 코드를 입력하세요
from sklearn.linear_model import LinearRegression
bagging_Linear = BaggingRegressor(base_estimator=LinearRegression(), n_estimators=100, random_state=SEED)
bagging_Linear_fitted = bagging_Linear.fit(x_train, y_train)
br_pred_linear = bagging_Linear_fitted.predict(x_test) # 코드를 입력해 주세요
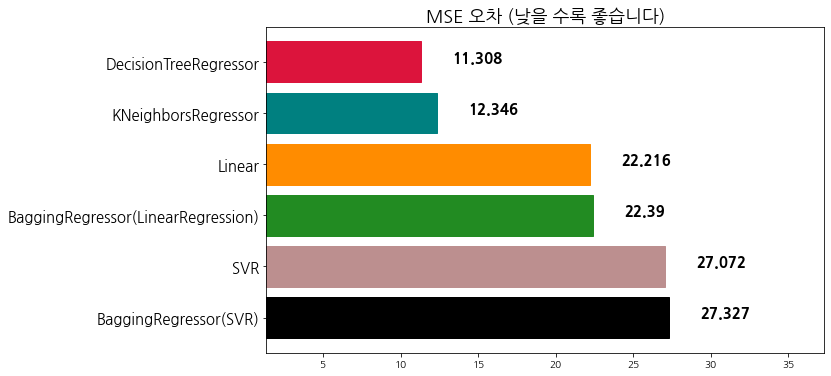
evaluate_prediction(br_pred_linear, 'BaggingRegressor(LinearRegression)')
algorithm mse
0 SVR 27.072338
1 BaggingRegressor(LinearRegression) 22.389916
2 Linear 22.215878
3 KNeighborsRegressor 12.345947
4 DecisionTreeRegressor 11.307961
Q3-2. base_estimator는 SVR
예측 결과 값은 br_pred_svr 변수에 대입해 주세요
# 코드를 입력해 주세요
from sklearn.svm import SVR
bagging_SVR = BaggingRegressor(base_estimator=SVR(), n_estimators=100, random_state=SEED)
bagging_SVR_fitted = bagging_SVR.fit(x_train, y_train)
br_pred_svr = bagging_SVR_fitted.predict(x_test) #코드를 입력해 주세요
evaluate_prediction(br_pred_svr, 'BaggingRegressor(SVR)')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 DecisionTreeRegressor 11.307961
Q3-3. base_estimator는 DecisionTreeRegressor
예측 결과 값은 br_pred_dcr 변수에 대입해 주세요
# 코드를 입력해 주세요
from sklearn.tree import DecisionTreeRegressor
bagging_DecisionTree = BaggingRegressor(base_estimator=DecisionTreeRegressor(), n_estimators=100, random_state=SEED)
bagging_DecisionTree_fitted = bagging_DecisionTree.fit(x_train, y_train)
br_pred_dcr = bagging_DecisionTree_fitted.predict(x_test) #코드를 입력해 주세요
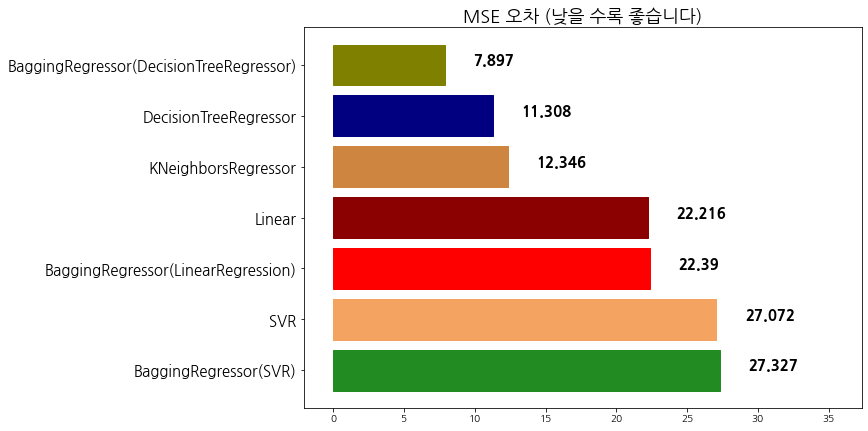
evaluate_prediction(br_pred_dcr, 'BaggingRegressor(DecisionTreeRegressor)')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 DecisionTreeRegressor 11.307961
6 BaggingRegressor(DecisionTreeRegressor) 7.897266
Q3-4. base_estimator는 KNeighborsRegressor
# 코드를 입력해 주세요
bagging_KNN = BaggingRegressor(base_estimator=KNeighborsRegressor(), n_estimators=100, random_state=SEED)
bagging_KNN_fitted = bagging_KNN.fit(x_train, y_train)
br_pred_knr = bagging_KNN_fitted.predict(x_test) #코드를 입력해 주세요
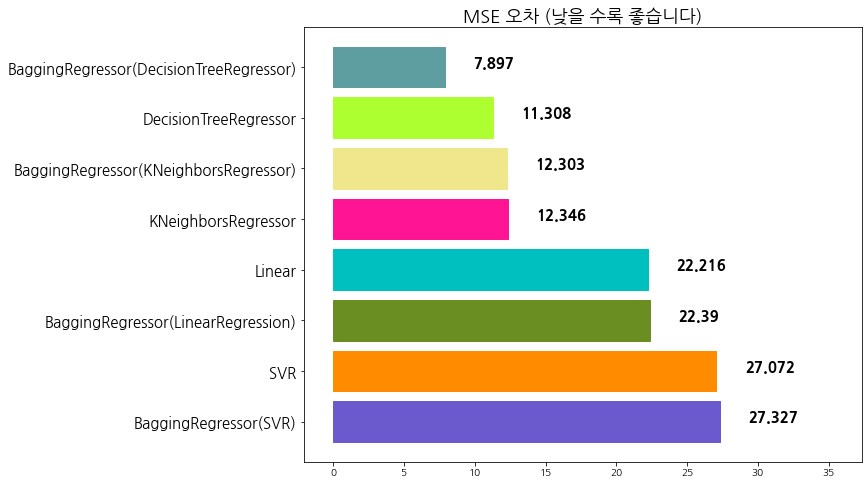
evaluate_prediction(br_pred_knr, 'BaggingRegressor(KNeighborsRegressor)')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
Q4. Random Forest
random_state=SEED 로 고정- RandomForestRegressor의
hyperparameter값 튜닝을 통해 목표 7.75 이하의 MSE를 기록합니다. - 예측한 결과를
rfr_pred변수에 할당
from sklearn.ensemble import RandomForestRegressor
## 코드를 입력하세요
random_forest_model1 = RandomForestRegressor(n_estimators = 138,
max_depth = 20,
random_state = SEED)
random_forest_model1_fitted = random_forest_model1.fit(x_train, y_train)
rfr_pred = random_forest_model1_fitted.predict(x_test) #코드를 입력해 주세요
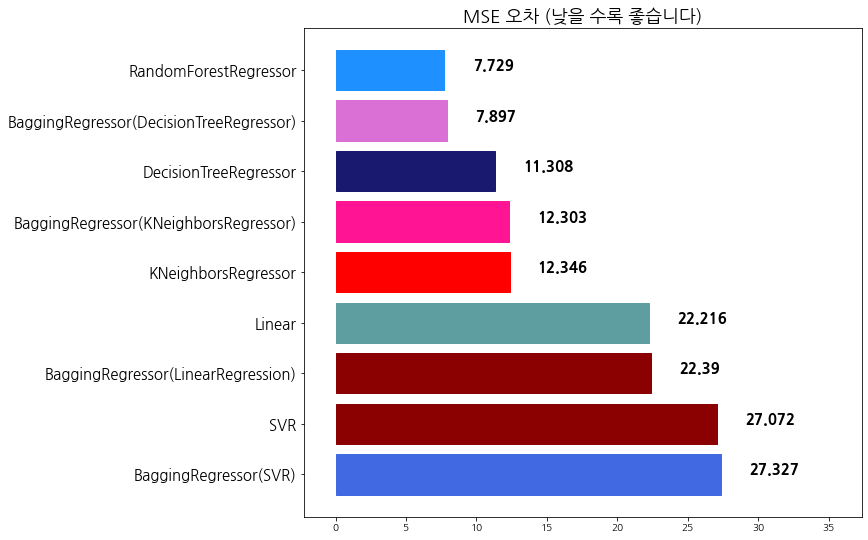
evaluate_prediction(rfr_pred, 'RandomForestRegressor')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
Boosting 앙상블
Boosting 알고리즘 역시 앙상블 학습 (ensemble learning)이며, 약한 학습기를 순차적으로 학습을 하되, 이전 학습에 대하여 잘못 예측된 데이터에 가중치를 부여해 오차를 보완해 나가는 방식 입니다.
다른 앙상블 기법과 가장 다른 점중 하나는 바로 순차적인 학습을 하며 weight를 부여해서 오차를 보완해 나간다는 점인데요. 순차적이기 때문에 병렬 처리에 어려움이 있고, 그렇기 때문에 다른 앙상블 대비 학습 시간이 오래걸린다는 단점이 있습니다.
더 많은 내용은 앙상블 학습(ensemble learning)으로 알고리즘 성능 개선하기 - Boosting 에서 확인할 수 있습니다.
Q5. AdaBoostRegressor
- AdaBoostRegressor를 활용하여 예측합니다.
n_estimators=100으로 고정합니다.base_estimators를 지정합니다.- 목표점수는 MSE 7.7 이하입니다.
abr_pred에 예측 값을 할당합니다.
from sklearn.ensemble import AdaBoostRegressor
# 코드를 입력해 주세요
tree_model = DecisionTreeRegressor(max_depth = 20)
Adaboost_model1 = AdaBoostRegressor( base_estimator = tree_model, # MSE 7.491
# base_estimator = DecisionTreeRegressor(), # MSE 7.7
# base_estimator = LinearRegression(), # MSE 29.928
# base_estimator = SVR(), # MSE 22.142
# base_estimator = KNeighborsRegressor(), # MSE 9.692
n_estimators = 100, # 100 고정
random_state = SEED) # 시드값 고정
Adaboost_model1_fitted = Adaboost_model1.fit(x_train, y_train)
abr_pred = Adaboost_model1_fitted.predict(x_test) # 코드를 입력해 주세요
evaluate_prediction(abr_pred, 'AdaBoostRegressor')
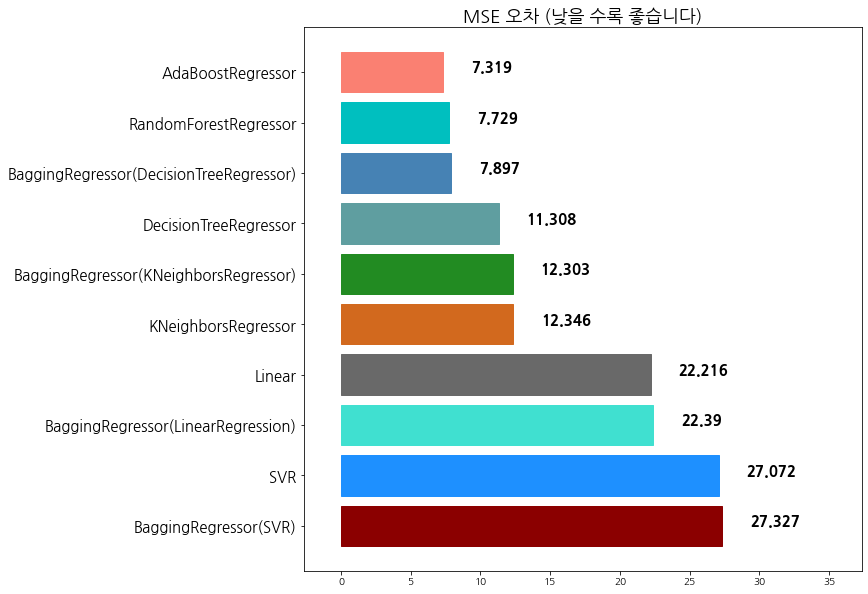
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
9 AdaBoostRegressor 7.318553
Q6. GradientBoostingRegressor
GradientBoostingRegressor를 활용하여 주택가격을 예측합니다.n_estimators,learning_rate,subsample파라미터를 조절하여 목표점수7.0 이하에 도전합니다.- 예측 후
gbr_pred변수에 예측 값을 할당 합니다.
learning_rate는 학습 속도를 조절합니다. 기본값은 1.0입니다.
subsample은 샘플데이터 활용 비율입니다. 기본값은 1이며, 1이면 모두 사용, 0.3이면 30%만 사용하겠다는 의미입니다.
from sklearn.ensemble import GradientBoostingRegressor
# 코드를 입력해 주세요
gbr_model1 = GradientBoostingRegressor( n_estimators=1000,
learning_rate=0.05,
subsample = 0.5,
random_state = SEED) # 시드값 고정
gbr_model1_fitted = gbr_model1.fit(x_train, y_train)
gbr_pred = gbr_model1_fitted.predict(x_test) # 코드를 입력해 주세요
evaluate_prediction(gbr_pred, 'GradientBoostingRegressor')
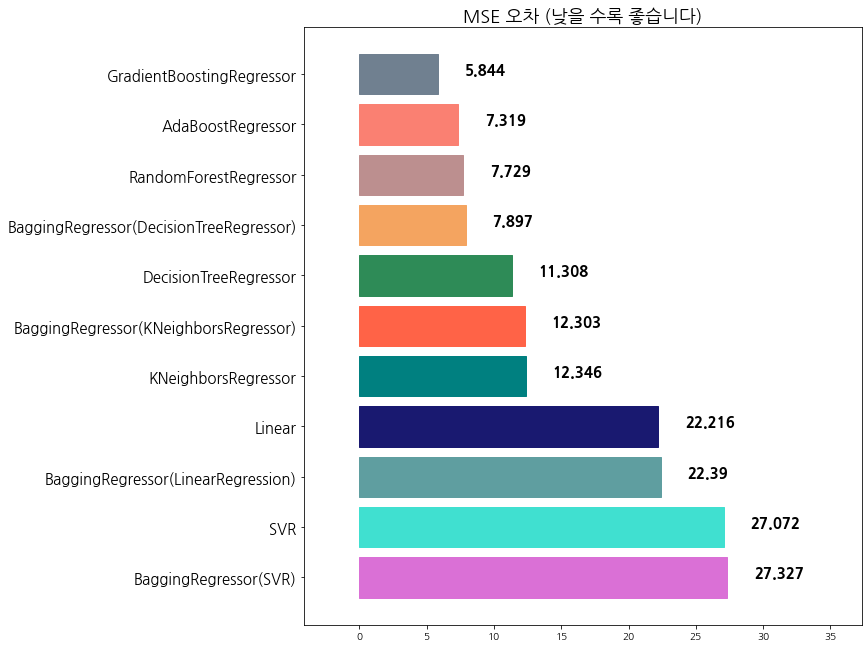
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
9 AdaBoostRegressor 7.318553
10 GradientBoostingRegressor 5.843941
Voting 앙상블
Voting은 단어 뜻 그대로 투표를 통해 결정하는 방식입니다.
Voting은 Bagging과 투표방식이라는 점에서 유사하지만, 다음과 같은 큰 차이점이 있습니다.
- Voting은 다른 알고리즘 model을 조합해서 사용합니다.
- Bagging은 같은 알고리즘 내에서 다른 sample 조합을 사용합니다.
더 많은 내용은 앙상블 학습(ensemble learning)으로 알고리즘 성능 개선하기 - Voting 에서 확인할 수 있습니다.
Q7. VotingRegressor
VotingRegressor를 활용하여 주택가격을 예측합니다.weights파라미터에는 각기 다른 weight를 적용하여, 베스트 조합을 찾습니다.- 현재까지 상위 4~5개 모델을 섞어
estimators로 사용합니다. - 목표점수는 6.8이하입니다.
from sklearn.ensemble import VotingRegressor
# 샘플 코드
# ensemble 할 model 정의
# estimators = [
# ('lin', LinearRegression()),
# ('rfr', RandomForestRegressor(n_estimators=100)),
# ('gbr', GradientBoostingRegressor()),
# ]
# 코드입력
estimators = [
# 앙상블 할 모델 정의
('gbr', gbr_model1),
('abr', Adaboost_model1),
('rfr', random_forest_model1),
('brd', bagging_DecisionTree),
('dtr', dtr),
]
weights=[10, 2, 1, 1, 1]
# 모델 학습
vr_model1 = VotingRegressor(estimators, weights)
vr_model1_fitted = vr_model1.fit(x_train, y_train)
vr_pred = vr_model1_fitted.predict(x_test) # 예측 값을 대입해 주세요
# 모델 평가
evaluate_prediction(vr_pred, 'VotingRegressor')
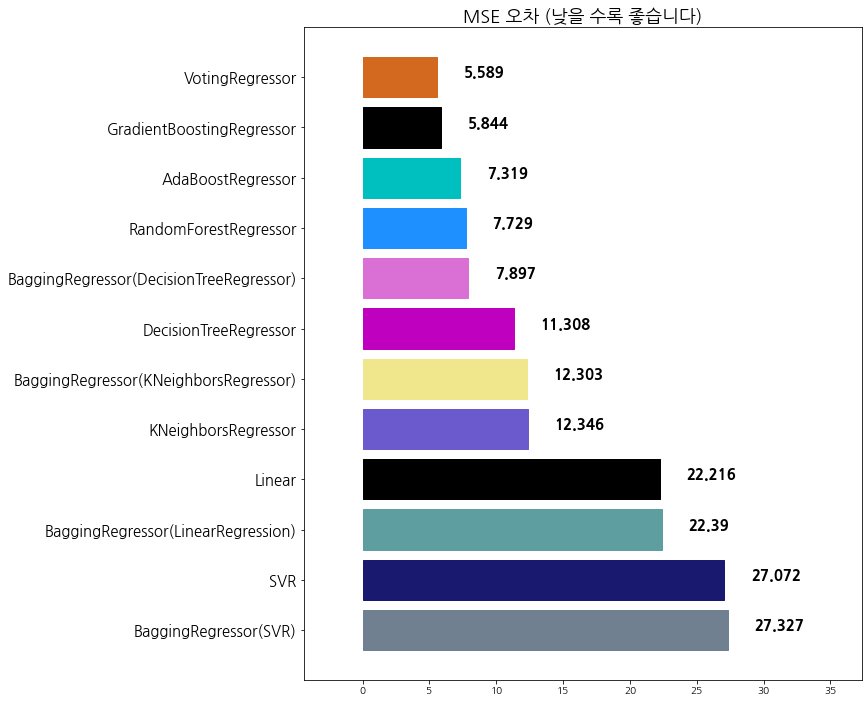
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
9 AdaBoostRegressor 7.318553
10 GradientBoostingRegressor 5.843941
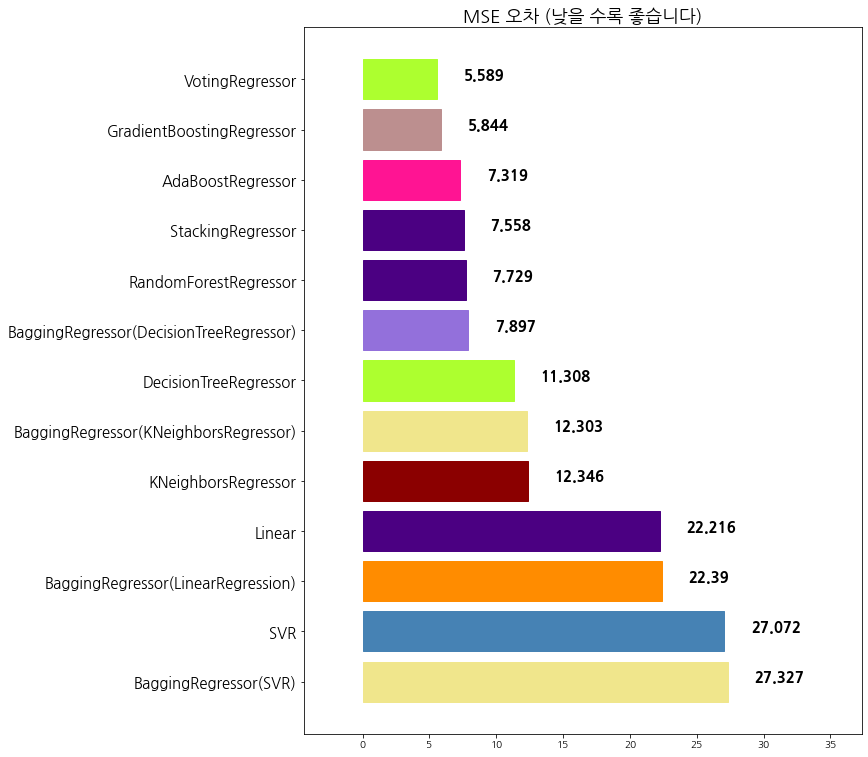
11 VotingRegressor 5.588586
Stacking 모델 쌓기
Stacking 앙상블은 대회에서 최고 점수에 도달하기 위하여 종종 사용되는 앙상블 기법입니다.
주요 특징은 개별 모델이 예측한 데이터를 토대로 다시 학습을 한다는 점입니다.
개별 모델이 예측한 데이터를 final_estimator가 최종 학습을 한 뒤 결과를 최종 예측합니다.
import sklearn
sklearn.__version__
'0.23.2'
StackingRegressor는 0.22 버전부터 추가되었습니다.
- pip install –upgrade -U scikit-learn
from sklearn.ensemble import StackingRegressor
'''
estimators = [
('abr', abr),
('br', br),
('rfr', rfr),
]
'''
reg = StackingRegressor(
estimators=estimators,
final_estimator=random_forest_model1, n_jobs=-1)
reg.fit(x_train, y_train)
stack_prediction = reg.predict(x_test)
evaluate_prediction(stack_prediction, 'StackingRegressor')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
9 StackingRegressor 7.557929
10 AdaBoostRegressor 7.318553
11 GradientBoostingRegressor 5.843941
12 VotingRegressor 5.588586
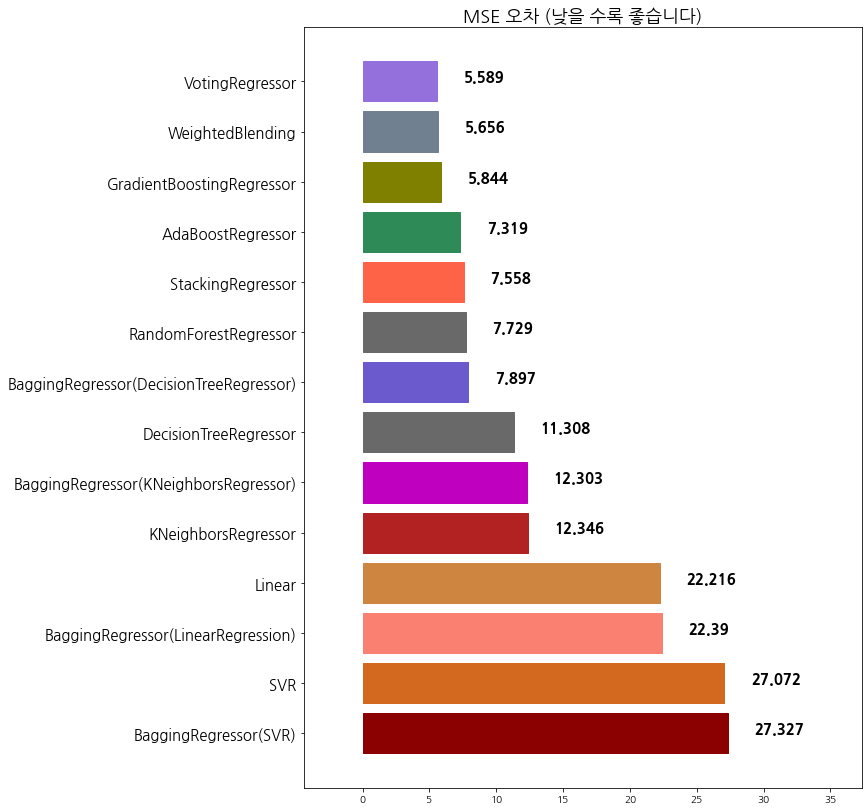
Weighted Blending 모델 혼합하기
Q8: Blending을 활용하여 최고 점수를 기록해 보세요
- weighted blending 기법은 말그대로 우리가 예측한 가격 값에 대하여, 일정한 비율 (weight)를 곱하여 최종 예측 값을 산출해 냅니다.
- weight의 총합은 1.0이 나와야 합니다.
- 일반적으로 좋은 성능이 나온 모델에 weight를 많이 부여합니다.
# 샘플코드
blend = gbr_pred * 0.4 + vr_pred * 0.4 + rfr_pred * 0.1 + abr_pred * 0.1
# 이곳에 여러분의 blending을 통해 최고 점수를 갱신해 보세요
blend = vr_pred * 0.4 + gbr_pred * 0.4 + abr_pred * 0.1 + rfr_pred * 0.1
evaluate_prediction(blend, 'WeightedBlending')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
9 StackingRegressor 7.557929
10 AdaBoostRegressor 7.318553
11 GradientBoostingRegressor 5.843941
12 WeightedBlending 5.655575
13 VotingRegressor 5.588586
Q9. 최종 과제: 각 종 모델을 앙상블하여 최고 점수에 도달하기
목표: MSE 점수를 6.3점 이하로 만들어 보세요
다양한 모델의 활용, voting, boosting, bagging, stacking, blending 등의 기법을 활용하여 최고 점수에 도달해 보세요!
evaluation predict 기준으로 6.3점 이하에 도전해 보세요.
# 이곳에 코드를 입력해 주세요
import lightgbm as lgb
from math import sqrt
from sklearn.metrics import mean_squared_error
lgb_dtrain = lgb.Dataset(data = x_train, label = y_train) # 학습 데이터를 LightGBM 모델에 맞게 변환
lgb_param = {'max_depth': 10, # 트리 깊이
'learning_rate': 0.01, # Step Size
'n_estimators': 1000, # Number of trees, 트리 생성 개수
'objective': 'regression'} # 목적 함수 (L2 Loss)
lgb_model = lgb.train(params = lgb_param, train_set = lgb_dtrain) # 학습 진행
lgb_model_predict = lgb_model.predict(x_test) # 평가 데이터 예측
print("RMSE: {}".format(sqrt(mean_squared_error(lgb_model_predict, y_test)))) # RMSE
RMSE: 2.7760424033106412
evaluate_prediction(lgb_model_predict, 'LightGBM')
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 BaggingRegressor(DecisionTreeRegressor) 7.897266
8 RandomForestRegressor 7.728578
9 LightGBM 7.706411
10 StackingRegressor 7.557929
11 AdaBoostRegressor 7.318553
12 GradientBoostingRegressor 5.843941
13 WeightedBlending 5.655575
14 VotingRegressor 5.588586
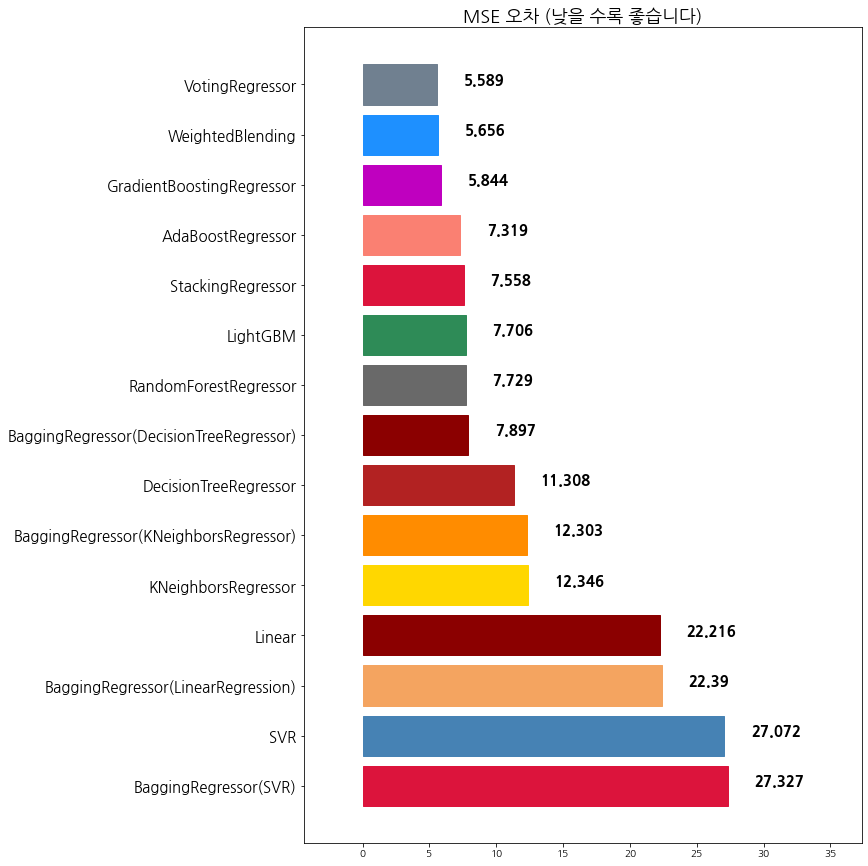
import xgboost as xgb
xgb_model = xgb.XGBRegressor(n_estimators=1000, learning_rate=0.01, gamma=0, subsample=0.75,
colsample_bytree=1, max_depth=10, random_state=SEED)
xgb_model_fitted = xgb_model.fit(x_train, y_train)
xgb_pred = xgb_model_fitted.predict(x_test) # 코드를 입력해 주세요
evaluate_prediction(xgb_pred, 'XGBoostRegression')
[16:55:15] WARNING: src/objective/regression_obj.cu:152: reg:linear is now deprecated in favor of reg:squarederror.
algorithm mse
0 BaggingRegressor(SVR) 27.327279
1 SVR 27.072338
2 BaggingRegressor(LinearRegression) 22.389916
3 Linear 22.215878
4 KNeighborsRegressor 12.345947
5 BaggingRegressor(KNeighborsRegressor) 12.303168
6 DecisionTreeRegressor 11.307961
7 XGBoostRegression 7.909719
8 BaggingRegressor(DecisionTreeRegressor) 7.897266
9 RandomForestRegressor 7.728578
10 LightGBM 7.706411
11 StackingRegressor 7.557929
12 AdaBoostRegressor 7.318553
13 GradientBoostingRegressor 5.843941
14 WeightedBlending 5.655575
15 VotingRegressor 5.588586